Recently Graph convolutional networks (GCNs) have gained significant interest in the deep learning world to solve problems with knowledge graphs (KGs) containing nodes, edges and relationships. Training a model to solve a problem with graph data is complex due to its multi-relational nature, types of relations, nodes, attributes and also noise when extracted from textual sources using natural language processing (NLP). Primarily two different kind of problems have been studied in KGs which are, node classification and link prediction and GCNs have been used to solve this problem following two different approaches; spectral and non-spectral.
With the spectral approach the learned filters of the GCNs depend on the spectral features of the graph and has been successfully used for node classification. On the other hand non-spectral approach defines convolutions directly on the graph operating on spatially close neighbours imposing the graph structure to the first order neighbours of a node. The latter is able to generalize to completely unseen graphs and suitable for inductive learning problems whereas the former cannot, due to its dependability on the spectral features.
Attention mechanisms have become the standard in many sequence based tasks in machine learning since its important to focus on specific and relevant parts of the input to make decisions and it also helps in the case of noisy input. A very recent work [1] has incorporated attention mechanism to GCNs in graph data using a non-spectral approach allowing it to generalise to unseen graph structures. This is named as Graph Attention Networks (GATs). The idea is to make sure that only specific edges in the graph are used in the training process which works well when there are many noisy edges. It learns attention weights that is informative of the usefulness of the edge. Lets see what happens in the attention layer.
The attention layer takes a set of input features for each node and outputs a set of features that is computed based on the attention mechanism applied. The input to this layer is a set of node features, it produces a new set of node features, as its output. A shared linear transformation given by a weight matrix W is applied to all nodes. Then self-attention is performed on all nodes by computing attention coefficients given by,
![\[e_{ij}= a(W\overrightarrow{h_i}, W\overrightarrow{h_j})\]](https://saatviga.com/wp-content/ql-cache/quicklatex.com-2448b368f3b96b5321bde70e43da0559_l3.png "Rendered by QuickLaTeX.com")
This tells the importance of node j to node i, but its computed only in the first-order neighbourhood (masked attention) and that’s where the graph structure is imposed in the model. The coefficients are normalised across all choices of j using the softmax function:
![\[\alpha_{ij}=softmax_{j}(e_{ij})=\frac{exp(e_{ij})}{\Sigma_{k\epsilon N_i}exp(e_{ik})}\]](https://saatviga.com/wp-content/ql-cache/quicklatex.com-53103aeb788b526b19e2a08cbeaf4696_l3.png "Rendered by QuickLaTeX.com")
The normalised coefficients are used to compute the final output features for every node in the attention layer after applying a non-linearity:
![\[\overrightarrow{h^{'}_i}=\sigma\left(\sum_{j\epsilon N_i}\alpha_{ij}W\overrightarrow{h_j}\right).\]](https://saatviga.com/wp-content/ql-cache/quicklatex.com-007274d93b79e3159f75a07f22925abf_l3.png "Rendered by QuickLaTeX.com")
In order to stabilise/normalise the process of attention, the authors also introduce multi-head attention, a process where several attention mechanisms are used to compute the attention coefficients and the average of them is used to compute the final output features of the nodes.
![\[\overrightarrow{h^{'}_i}=\sigma\left(\frac{1}{K}\sum^{K}_{k=1}\sum_{j\epsilon N_i}\alpha^{k}_{ij}W^{k}\overrightarrow{h_j}\right)\]](https://saatviga.com/wp-content/ql-cache/quicklatex.com-159e7dd3c404a2990ea613ba4424ec3d_l3.png "Rendered by QuickLaTeX.com")
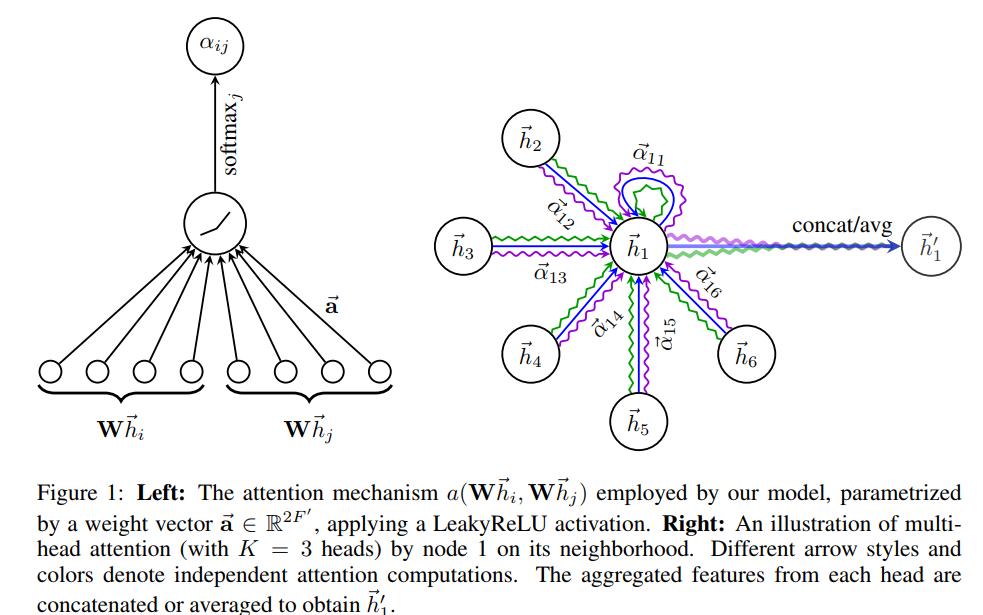
The figure (left) shows the model being parameterized by an attention vector and how multi-head attention (right)is employed to aggregate the final output of the attention layer. The key contribution of this work is that since a shared attention mechanism is applied to the edges, it does not depend on the graph structure (like in previous models like GCNs which is based on the laplacian eigenbasis of the graph), enabling the model to be used in inductive learning tasks while also the learned attention weights enable more interpretability of the results showing the importance of an edge in a link prediction task.
Reference:
[1] Veličković, P., Cucurull, G., Casanova, A., Romero, A., Lio, P., & Bengio, Y. (2017). Graph attention networks. arXiv preprint arXiv:1710.10903.
